accueil / sommaire cours terminale S / suites majorées, minorées et bornées
V Suites majorées, minorées et bornées
Soit (un)n≥a une suite à termes réels, elle est majorée (respectivement minorée) s'il existe une constante M (respectivement m) telque pour tout entier n ≥ a on a un ≤ M (respectivement un ≥ m).
M est alors un mojorant de la suite et m est alors un minorant de la suite.
La suite est bornée si majorée et minorée alors il existe une constante μ ≥ 0 telque pour tout entier n ≥ a,
∣ un∣ ≥ μ.
1) Comparaison directe de un à M ou à m
exemple :
Soit U = (un)n≥0 telque pour tout n ≥ 0 on a un = (2n + 1)÷(n + 1)
Montrer que la suite U est majorée par 2.
Pour tout entier n ≥ 0 un − 2 = − 1 ÷ (n + 1) < 0
Conclusion : pour tout entier n ≥ 0 un < 2 CQFD.
2) Suite donnée de manière explicite
Par un = ƒ(n), ƒ étant une fonction numérique définie sur [a; +∞[. L'etude des variation de ƒ sur son domaine permet évantuellement de trouver un majorant ou un minorant de ƒ sur [a; +∞[ donc de la suite.
exemple :
Soit U = (un)n≥0 telque pour tout n ≥ 0 on a un = (3n − 5)÷(2n + 1)
et la fonction ƒ : ℜ → ℜ x →ƒ(x) = 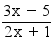 on a Dƒ = ℜ\{−1/2}.
on a Dƒ = ℜ\{−1/2}.
Pour tout entier n ≥ 0 un = ƒ(n) on a [0;+∞[ ⊂ Dƒ.
Pour tout x ∈ Dƒ, ƒ'(x) =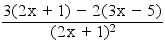 =
= 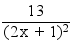 > 0
> 0
donc ƒ est strictement croissante sur [0;+∞[ .
On a ƒ(0) = − 5 et limx→+∞ƒ(x) = 3/2 donc ∀ x ∈ ℕ ƒ(x) ∈ [− 5;3/2] .
Conclusion : la suite U est bornée, elle est majorée par 3/2 et minorée par − 5.
3) Cas des suites récurrentes
exemple :
Soit U = (un)n≥0 définie par :
u0 = λ = constante ∈ [0;1/2] et ∀ n ∈ ℕ, un+1 = un2 + un ÷ 2 = ![]() .
.
Montrons que ∀ n ∈ ℕ, un ∈ [0;1/2].
Par récurrence :
Soit P(n) l'énoncé " un ∈ [0;1/2] ".
P(0) est vrai.
Soit n un entier ≥ 0 quelconque telque P(n) soit vrai, c'est-à-dire que 0 ≤ un ≤ 1/2 (hypothèse de récurrence).
Montrons que P(n+1) est vrai c'est à dire c'est-à-dire que 0 ≤ un+1 ≤ 1/2 .
démonstration :
Nous avons 0 ≤ un ≤ 1/2
d'où 0 ≤ un2 ≤ 1/4 et aussi 0 ≤ un ÷ 2 ≤ 1/4
d'où
0 ≤ un2 + un ÷ 2 ≤ 1/4 + 1/4
0 ≤ un2 + un ÷ 2 ≤ 1/2
0 ≤ un+1 ≤ 1/2
donc P(n+1) est vrai.
conclusion : P(0) est vrai et P(n+1) Iest vrai donc l'enoncé de récurrence est vrai et nous avons montré que un ∈ [0;1/2] pour tout n entier naturel positif.
Autre méthode :
La suite est récurrente, soit la fonction ƒ ℜ → ℜ : x →ƒ(x) = ²x + x/2, la suite est alors définie par :
u0 = λ = constante ∈ [0;1/2] et ∀ n ∈ ℕ, un+1 =ƒ(un).
I = [0;1/2]
Pour tout n entier naturel un ∈ [0;1/2], il suffit de vérifier que :
u0 ∈ I et ƒ(I) ⊂ I c'est-à-dire ∀ x ∈ I , ƒ(x) ∈ I.
En effet, nous avons u0 ∈ [0;1/2] et pour tout n ≥ 0 telque un ∈ [0;1/2] alors un+1 = ƒ(un) ∈ ƒ([0;1/2])
d'où un+1 ∈ ƒ([0;1/2]) .
Pour établir ƒ(I) ⊂ I, on étudie les variations de ƒ sur I. ƒ est continue dérivable sur I .
∀ x ∈ I , ƒ'(x) = 2x + 1/2 > 0 , donc ƒ est strictement croissante sur I donc ƒ(I) = [ƒ(0);ƒ(1/2)] = [0;1/2]
donc ƒ(I) ⊂ I CQFD .
Conclusion : on a bien ∀ n ∈ ℕ, 0 ≤ un ≤ 1/2 la suite est bornée.
4) Généralisation
Soit U = (un)n≥a la suite à termes réels définie par son premier terme ua et par la relation :
∀ n ≥ a un+1 = ƒ(un), ƒ étant une fonction numérique donnée.
Si nous voulons montrer que pour n entier ≥ a , un ∈ I. I étant un intervalle donné inclus dans le domaine de définition.
Nous pouvons utiliser la méthode suivante :
i) vérifier que ua ∈ I
ii) vérifier si ƒ(I) ⊂ I par exemple en étudiant les varations de ƒ sur I ou en grâce à une récurrence.